Greedy Algorithm Explained

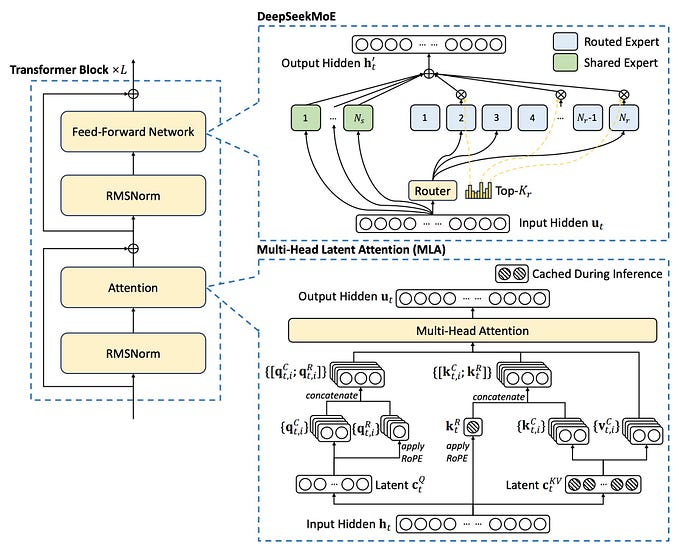
A greedy algorithm is an algorithmic paradigm that follows the problem-solving heuristic of making the locally optimal choice at each stage with the hope of finding a global optimum. In other words, a greedy algorithm makes the best possible decision at each step by considering only the current situation, without worrying about the consequences of future decisions.

Here’s an example of a greedy algorithm in Go for solving the coin change problem:

package main

import "fmt"

func main() {
    // Define the coin values and the target amount
    coins := []int{1, 5, 10, 25}
    amount := 31

    // Initialize the result
    result := 0

    // Iterate through the coins in descending order
    for i := len(coins) - 1; i >= 0; i-- {
        // Calculate the number of coins needed
        n := amount / coins[i]

        // Update the result and the amount
        result += n
        amount -= n * coins[i]
    }

    // Print the result
    fmt.Println(result)
}

In this example, we define an array of coin values and a target amount. We then iterate through the coin values in descending order and calculate the number of coins needed to reach the target amount. We update the result and the remaining amount at each step, and print the final result.

Here’s how this greedy algorithm works:

1. Define the coin values and the target amount.
2. Initialize the result to 0.
3. Iterate through the coin values in descending order.
4. Calculate the number of coins needed to reach the target amount.
5. Update the result and the remaining amount.
6. Repeat steps 4 and 5 until the remaining amount is 0.
7. Print the result.

The greedy algorithm for the coin change problem works by always choosing the coin with the highest value, as long as it doesn’t exceed the remaining amount. This means that it will always make the best possible choice at each step, with the hope of finding the global optimum.

Of course, not all problems can be solved using a greedy algorithm, and it is important to carefully evaluate the trade-offs of using a greedy algorithm before implementing one. However, when used appropriately, greedy algorithms can be an effective tool for solving optimization problems.